NeRF
基本概念
相关链接
广义理解
NeRF通过神经网络(MLP多层感知机)来隐式的存储$3D$信息。
- 显式的$3D$信息:有明确的$x,y,z$值。
- 隐式的$3D$信息:无明确的$x,y,z$的值,只能输出指定角度的$2D$图片。
也因此,模型并不具备泛化能力,一个模型只能存储一个$3D$信息。
模型结构
论文中模型的输入是一个$5D$的向量$(x,y,z,\theta,\phi)$,分别是坐标值、方位角、仰角。输出是$4D$向量,分别是密度和颜色(RGB)。模型的结构是一个$8$层的MLP。
NeRF的模型结构比较简单,重点在于是前处理和后处理。对于输入,需要有一个图片转$5D$的前处理;对于输出,需要有一个$4D$转图片的后处理。
实际上,输入的$5D$向量是粒子的空间位姿,输出的$4D$向量是粒子对应的颜色以及密度。
真实场景及相机模型
真实场景
现实生活中有多个光源,同时会有物体的折射和反射。
相机模型
相机模型连接了$3D$世界与$2D$图片,主要分为四个坐标系:
- 世界坐标系:现实世界的三维坐标系,相当于地球的经纬度。
- 相机坐标系:以相机镜头中心为原点的三维坐标系,通过相机的位置+朝向将世界坐标转换过来。
- 归一化相机坐标系:把相机前方的空间压缩成一个固定边长的立方体(一般为2),统一不同距离的物体缩放比例。
- 像素坐标系:最终照片上的像素网格位置。
体渲染
定义
- 属于渲染技术的分支
- 目的是解决云/烟/果冻等非刚性物体的渲染建模
- 将物质抽象成一团飘忽不定的粒子群
- 光线在穿过时,是光子在跟粒子发生碰撞的过程
光子与粒子发生作用的过程
- 吸收:光子被粒子吸收
- 放射:粒子本身发光
- 外射光:光子在冲击后,被弹射
- 内射光:其他方向弹射来的粒子。
NeRF假设
- 物体是一团自发光的粒子
- 粒子有密度和颜色
- 外射光和内射光抵消
- 多个粒子被渲染成指定角度的图片
模型的输入输出
模型的输入:将物体进行稀疏表示的单个粒子的位姿。
模型的输出:该粒子的密度和颜色。
粒子的采集-光线原理
射线推导像素点
对于空间中的一个发光粒子:
- 空间坐标$(x, y, z)$
- 发射的光线通过相机模型
- 成为图片上的像素坐标$(u, v)$
- 粒子颜色即为像素颜色
其中$(u, v)$与$(x, y, z)$的公式如下:
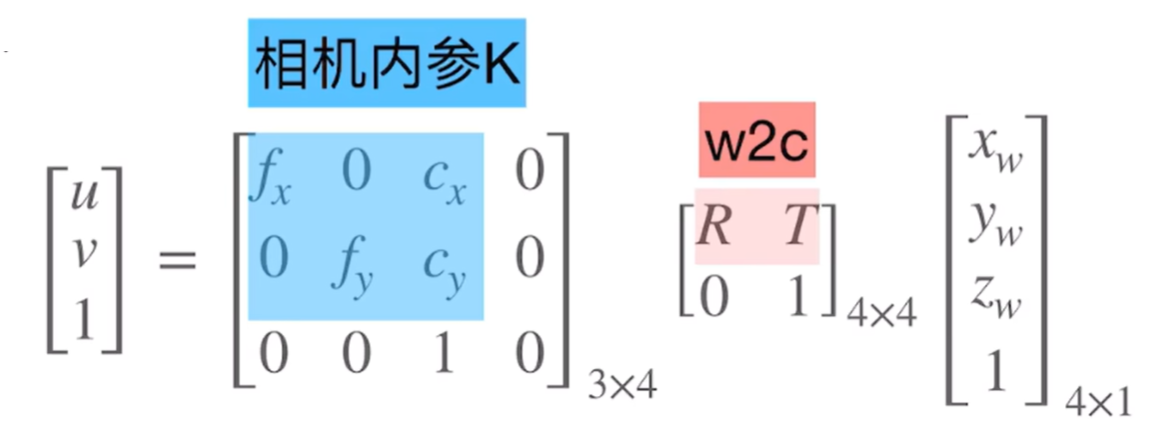
其中$R$为旋转矩阵$(3\times 3)$,$T$为平移向量$(3\times 1)$。
反之,对于图片上的某一个像素$(u, v)$的颜色。可以看作是沿着某一条射线上的无数个发光点的“和”,利用相机模型,反推射线,那么这个射线表示为:
$$
r(t)=o+t\vec{d}
$$
其中$o$为射线原点,$\vec{d}$为方向,$t$为距离,使用极坐标的方法表示。理论上来讲,$t$的取值范围为$(0,+\infty)$。
对于一张大小为$(H, W)$的图片而言,其射线数量为$H\times W$。
像素点推导射线
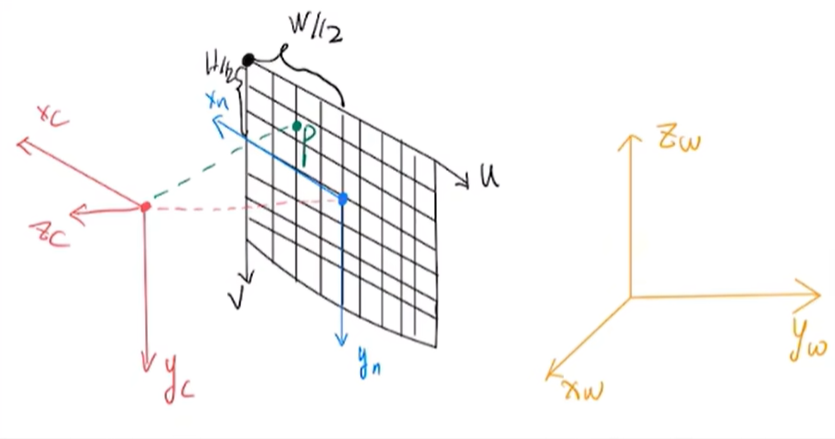
由像素点$P(u, v)$反推射线基本过程如下。
像素平面$\to$物理成像平面:
$$
(x_n,y_n)=(-(u-\frac{w}{2}),v-\frac{h}{2})=(\frac{w}{2}-u,v-\frac{h}{2})
$$
物理成像平面$\to$相机坐标系:
$$
(x_c,y_c,z_c)=(x_n,y_n,-f)
$$
其中$f$为相机焦距。
归一化:
$$
(x_c,y_c,z_c)=(\frac{x_c}{f},\frac{y_c}{f},-1)
$$
相机坐标系$\to$世界坐标系:
$$
(x_w,y_w,z_w)=c2w\times(x_c,y_c,z_c)
$$
坐标转换代码
1 | # Ray helpers |
这个方法一共有四个参数,$H$和$W$表示图像的大小,$K$表示相机的内参,$c2w$表示旋转矩阵和平移向量。
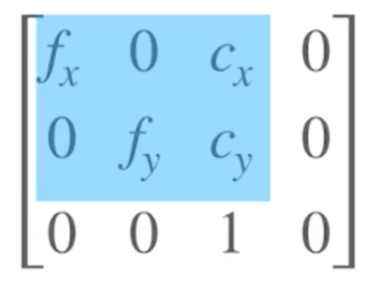
其中,$K[0][2]$和$K[1][2]$分别表示光心在图像中的$x$坐标和$y$坐标,可以通过这两个值确定成像中心的位置。
因此有如下公式:
$$
K[0][2]=\frac{W}{2}
$$
$$
K[1][2]=\frac{H}{2}
$$
$f_x$和$f_y$分别表示$x$轴的焦距和$y$轴的焦距,可以控制水平方向和垂直方向的成像尺度。
如果这两个值相等,那么就是正方形像素,如果二者不等,那么图像会被拉伸变形。
也就是说,对于NeRF而言,有如下关系:
$$
f_x=f_y=f
$$
1 | i, j = torch.meshgrid(torch.linspace(0, W-1, W), torch.linspace(0, H-1, H)) # pytorch's meshgrid has indexing='ij' |
这段代码的主要功能是把像素平面转换为相机坐标系并进行归一化处理。
相对于像素点推导射线的公式而言,代码中与其有一定区别。上述$u$与$x_n$方向相反,$v$与$y_n$方向相同;而在代码中,$u$与$x_n$方向相同,$v$与$y_n$方向相反。
$i$和$j$分别表示图像的$u$方向和$v$方向,根据之前的公式推导,我们可以得出,转换后的坐标如下所示:
$$
(x_c,y_c,z_c)=(\frac{x_c}{f},\frac{y_c}{f},-1)=(u-\frac{w}{2},-(v-\frac{h}{2}),-1)
$$
该公式与上述公式相反的原因是坐标轴方向的变化。
那么推导一下就可以得出:
$$
(x_c,y_c,z_c)=(\frac{x_c}{f},\frac{y_c}{f},-1)=(i-\frac{W}{2},-(j-\frac{H}{2}),-1)
$$
再通过代码torch.stack(tensors, dim=0)就可以将多个张量沿着一个新维度拼接起来。
1 | # Rotate ray directions from camera frame to the world frame |
dirs是相机坐标系的方向,通过与c2w矩阵的旋转矩阵部分相乘,可以得到世界坐标系的方向,也就是rays_d。
同理,rays_o是平移光线原点,取的是c2w矩阵中的平移向量部分。
训练取样代码
1 | coords = torch.reshape(coords, [-1,2]) # (H * W, 2) |
这部分代码是选取batch进行训练,如果选用一张图片上的所有像素点(射线)进行训练,那样会非常缓慢。为了解决这一问题,可以采用随机采样的方法,从而加快训练速度。
1 | coords = torch.reshape(coords, [-1,2]) # (H * W, 2) |
这段代码可以将像素坐标展成一维列表,方便进行采样。
1 | select_inds = np.random.choice(coords.shape[0], size=[N_rand], replace=False) # (N_rand,) |
这段代码进行不重复随机采样,采样数量取决于预先设定的值。
1 | select_coords = coords[select_inds].long() # (N_rand, 2) |
在随机取样后,需要索引具体的像素点坐标,long可以保证坐标值为整数。
1 | rays_o = rays_o[select_coords[:, 0], select_coords[:, 1]] # (N_rand, 3) |
在这之后,就可以获取到采样点的o值和d值,也就是射线的起点和方向。
1 | batch_rays = torch.stack([rays_o, rays_d], 0) |
将随机采样的点打包处理,方便后续进行训练。
1 | target_s = target[select_coords[:, 0], select_coords[:, 1]] # (N_rand, 3) |
最后,获取这些点的颜色信息并存储。
粒子采样
实际中的$t$是连续的,但是计算机做不到连续,因此实际上在计算机中的$t$是离散的。可以在某个区间中对粒子进行随机采样,这个near和far可以调参更改,论文中选用的是near=2, far=6。在这之间进行均匀采样,共采样了$64$个点。
事实证明,标准的均匀采样效果并不如加入波动值的采样结果,加入一点波动值可以有效提高模型的鲁棒性,从而产生更好的效果。不含有扰动的采样公式为:
$$
t_i=U[t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)]
$$
粒子采样代码
1 | near, far = near * torch.ones_like(rays_d[...,:1]), far * torch.ones_like(rays_d[...,:1]) |
这部分代码主要是对粒子进行采样并增加了一部分扰动。
1 | near, far = near * torch.ones_like(rays_d[...,:1]), far * torch.ones_like(rays_d[...,:1]) |
这部分代码将标量near和far扩展到与光线方向张量相同的形状。rays_d[...,:1]取光线方向的第一个分量但保持形状,然后创建相同形状的全1张量,实现批量处理每条光线的近远平面距离。这里只是为了创建形状、维度相同的张量,因此只需要取第一个分量,并不关心具体值,只关心其形状。
1 | t_vals = torch.linspace(0., 1., steps=N_samples) |
这段代码创建0到1之间的均匀采样比例序列,用于后续计算具体深度值。
1 | if not lindisp: |
根据是否使用线性视差(lindisp)选择深度计算方式:
- 线性深度模式:直接在物理空间均匀采样(适合室内/物体重建)
- 视差线性模式:在透视空间均匀采样(适合全景场景,近处更密集)
1 | z_vals = z_vals.expand([N_rays, N_samples]) |
将维度扩展为射线数乘采样点数。
1 | if perturb > 0.: |
这段代码实现了NeRF中分层随机扰动采样的核心逻辑,让采样点不再均匀分布,而是引入随机性以提升模型表达能力。
首先计算每对相邻采样点之间的中点,接着拼接出每一个区间段的上界和下界。上界构成是中点外加最后一个点;下界构成是第一个点外加中点。接着定义一个相同维度的张量存储随机因子,测试模式下,采用相同的随机种子,为每一个区间生成一个随机因子。最后去计算每个区间的波动,成功对粒子进行采样。
我们来重点看一下这句代码:
1 | mids = .5 * (z_vals[...,1:] + z_vals[...,:-1]) |
这句代码进行了切片,第一个切片是第二个值到最后一个值;第一个切片是第一个值到最后一个值。第一个切片可以理解为每一个区间段的上界,第二个是每一个区间段的下界,二者相加求平均就是每一段的中点。
1 | pts = rays_o[...,None,:] + rays_d[...,None,:] * z_vals[...,:,None] # [N_rays, N_samples, 3] |
最后这段代码根据之前的公式:
$$
r(t)=o+t\vec{d}
$$
将每一个粒子的深度值代入,就可以求出其在世界坐标系下的坐标。
模型输入总结
NeRF模型的输入是图片,根据图片的每个像素点和相机的位姿计算出若干条射线(射线总数是图片的像素点个数),接着在每条射线上取若干个粒子。
具体而言,需要将像素点转换为世界坐标系下的坐标点,接着使用c2w的平移向量推算出相机的原点(世界坐标系下),这样就获得了这条射线上的两个点,分别为$(x_0,y_0,z_0)$和$(x_1,y_1,z_1)$,也就是相机原点和像素点在世界坐标系下的坐标。那么方向坐标其实就是$(x_1-x_0,y_1-y_0,z_1-z_0)$,也就是模型输入中的仰角和方位角(实际上这两个参数对应的是三个方向坐标,也就是三个参数)。每条射线上取若干个粒子,根据上述得到的$o$和$d$的值,对每条射线进行随机取样(均匀取样的基础上增加扰动值),得到每条射线取样数乘射线数的粒子个数,通过公式$r(t)=o+t\vec{d}$计算出每个粒子的世界坐标系坐标,每个粒子对应一组$(x,y,z)$坐标。
总而言之,一张图片上取$a$个像素,一共得到了$a$条射线,每条射线上采样了$b$个粒子,因此一共有$ab$个粒子,这些粒子以batch的形式输入到模型中。
根据上述可知,输入的张量为$[ab,3]$,每个粒子均有一组$(x,y,z)$坐标;同时还需要输入仰角和方位角$(ray_d)$,对应5D输入的$\theta$和$\phi$,这个方位本质上是$(x_1-x_0,y_1-y_0,z_1-z_0)$,因此5D输入也可以看做是6D输入。
模型输入代码
1 | viewdirs = rays_d |
这段代码是对方向向量的归一化操作,方便后续计算。首先创建了方向向量的副本,防止直接修改原数据。
torch.norm(viewdirs, dim=-1, keepdim=True)的作用是计算向量的长度,keepdim是为了保持相同的维度。
进行归一化操作可以避免长度变化影响网络学习,同时统一方向输入的数值范围。
最后将其形状转换为二维矩阵,大小为$(N, 3)$,其中$N$为射线数量,$-1$可以保证自动计算维度大小。
1 | raw = network_query_fn(pts, viewdirs, network_fn) |
这部分代码是神经网络前向传播,其中network_fn是模型函数;pts是一个$(a,b,3)$的张量;$a$表示采样的射线数,$b$表示每条射线采样的粒子数,$3$表示该粒子的世界坐标。viewdirs是一个$(a,3)$的张量,$a$表示采样的射线数,$3$表示方位,其本质是射线上的一个点与相机原点构成的射线的方位,射线上选的点是归一化之后的世界坐标。
模型结构
NeRF的模型结构比较简单,主体是一个$8$层的全连接层。
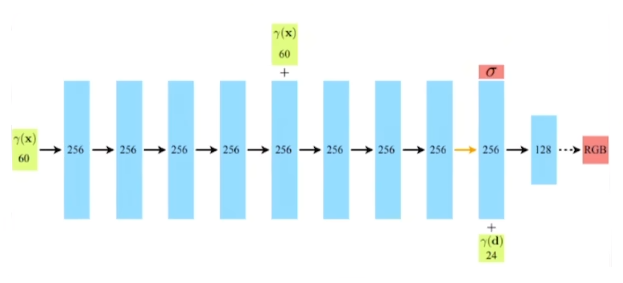
输入是一个$60$维的位置坐标,中间再次输入位置坐标。后半路会输出密度$\sigma$,同时输入$24$维的方向视角,最后输出颜色RGB。
位置编码
编码维度
这里会发现一个问题,前文中位置坐标和方向视角都是$3$维的,但是在这里就变成了$60$维和$24$维。
这是因为在实验过程中发现,当只输入3D视角和3D位置时,建模结果细节丢失,缺乏高频信息。

第一张图是真实数据,第二张图是完整模型的结果,第四张图是没有位置编码的结果。可以看出,如果缺少高频信息,那么细节部分会严重丢失。
为了解决这一问题,引入了位置编码:
$$
\gamma(p)=(sin(2^0\pi p),cos(2^0\pi p),\dots,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p))
$$
在这个公式中,$p$需要归一化到$[-1,1]$,每一个$L$分别对应了一个$sin$和一个$cos$。
对于空间坐标而言,$L=10$,$\gamma(\vec{x})$是$60D$;对于视角坐标而言,$L=4$,$\gamma(\vec{d})$是$24D$。
在代码中,实际上还加上了初始值,由于初始值各为$3D$,故$\gamma(\vec{x})$是$63D$,$\gamma(\vec{d})$是$27D$。
$L$实际上是一个超参数,并不是固定值。一般而言,空间坐标的重要性大于视角坐标,在模型结构中可以看到输出密度信息时,还没有加入方向的信息。其流程为先输出了密度,再加入了视角坐标,最终得到颜色。也就是说,只有颜色才与视角信息相关,密度信息只取决于坐标信息。颜色在各个角度观测是不一样的,因此才和角度相关。
核心原因
原始的$3D$坐标是低频平滑信号(位置连续渐变),视角方向也是低频连续变化量,二者都是低频输入。
而MLP(多层感知机)被证明具有频谱偏差,天然倾向学习低频函数。如果直接输入原始的坐标,那么网络会偏好平滑插值,这样就导致了细节的丢失。
网络分析
根据上述分析,可以知道,最开始的输入层是$63D$的信息;接下来的四层每一层均为$256D$;在第六层原有$256D$的基础上,又增加了$63D$的高频位置编码;最后一层添加了$27D$的高频方向编码,输入为$283D$,输出层是$128D$。
Loss
NeRF中采用自监督学习的方式,$GT$(标准答案)是图片中某一像素点的真实颜色值,将该像素对应光线上的粒子颜色进行求和,得到的是该像素颜色的预测值。
$MSE$指的是均方误差:
$$
MSE=\frac{1}{n}\sum^n_{i=1}(预测值_i-真实值_i)^2
$$
对于NeRF而言,相当于如下公式:
$$
L=\sum_{r\in R}\lVert {\hat C(r)-(r)} \rVert ^2_2
$$
其中$R$表示的是每个batch的射线数,一般为$1024$条。
可以对上述公式进行拆分:
$$
\sum_{r\in R}\lVert {\hat C(r)-(r)} \rVert ^2_2=(\sqrt {(\hat{R}-R)^2+(\hat{G}-G)^2+(\hat{B}-B)^2})^2
$$
再次化简可以得到:
$$
L=(\hat{R}-R)^2+(\hat{G}-G)^2+(\hat{B}-B)^2
$$
体渲染-连续积分
这部分解决的问题是将光线上的粒子颜色进行求和运算,核心公式为:
$$
\hat{C(s)}=\int^{+\infty}_{0}T(s)\sigma(s)C(s)ds
$$
$$
T(s)=e^{-\int^s_0\sigma(t)dt}
$$
在上述公式中:
- $T(S)$:在$s$点之前,光线没有被阻碍的概率。
- $\sigma(s)$:在$s$点处,光线碰击粒子(光线被粒子阻碍)的概率密度。
- $C(s)$:在$s$点处,粒子光的颜色。
简单理解为,预测颜色等于每个点的不透明度、体密度和颜色的乘积。
每个点的颜色和概率密度是已知的,可以由模型输出得到,因此需要求$T(s)$。
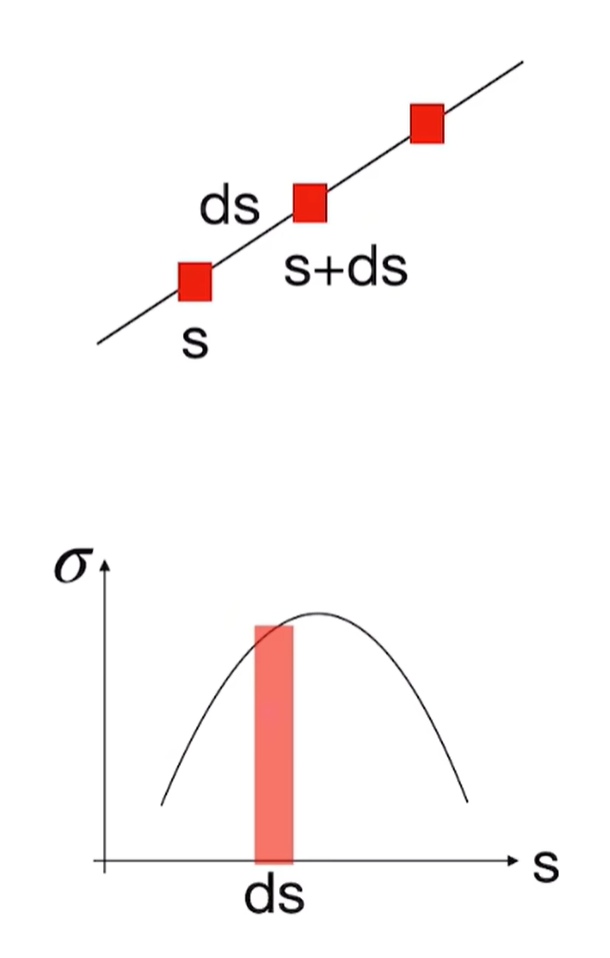
由于在每个点处光线被阻碍是独立事件,$\sigma(s)$表示光线被阻挡的概率,那么$1-\sigma(s)$表示光线没有被阻挡的概率,因此有如下结论:
$$
T(s+ds)=T(s)[1-\sigma(s)ds]
$$
将右侧展开得到:
$$
T(s+ds)=T(s)-T(s)\sigma(s)ds
$$
移项得到:
$$
T(s+ds)-T(s)=-T(s)\sigma(s)ds
$$
根据微分的定义可知:
$$
T(s+ds)-T(s)=dT(s)
$$
因此原式可变为:
$$
dT(s)=-T(s)\sigma(s)ds
$$
两边同时除以$T(s)$可变为:
$$
\frac{dT(s)}{T(s)}=-\sigma(s)ds
$$
两边同时积分:
$$
\int^t_0\frac{dT(s)}{T(s)}=\int^t_0-\sigma(s)ds
$$
化简得:
$$
\int^t_0\frac{1}{T(s)}dT(s)=\int^t_0-\sigma(s)ds
$$
求出左边部分:
$$
lnT(s)|^t_0=\int^t_0-\sigma(s)ds
$$
接着计算左侧部分:
$$
lnT(t)-lnT(0)=\int^t_0-\sigma(s)ds
$$
$T(0)$表示的是在位置为$0$的点之前,光线没有被阻挡的概率,很显然,概率为$1$,故$lnT(0)=ln1=0$,因此有如下公式:
$$
lnT(t)=\int^t_0-\sigma(s)ds
$$
两边同时取$e$,得到:
$$
T(t)=e^{-\int^t_0\sigma(s)ds}
$$
代换一下变量,可以得到最终结果:
$$
T(s)=e^{-\int^s_0\sigma(t)dt}
$$
体渲染-离散积分
数学推导
由于计算机只能处理离散化的数据,因此将光线$[0,s]$划分为$N$个等间距区间$T_n\to T_{n+1}$,间隔长度为$\delta_n$,同时假设区间内密度$\sigma_n$和颜色$C_n$颜色固定。
因此可以得到如下公式:
$$
\hat{C}(r)=\sum^N_{i=1}T_i(1-e^{-\sigma_i\delta_i})C_i
$$
$$
where\ T_i=e^{\sum_{j=1}^{i-1}\sigma_j\delta_j}
$$
我们可以来推导一下这个公式,本质上离散化是对每个光区贡献光强进行累加:
$$
\hat{C} = \sum^N_{n=0} I(T_{n} \to T_{n+1})
$$
其中:
$$
I(T_n \to T_{n+1}) = \int_{t_n}^{t_{n+1}} T(t) \sigma_n C_ndt
$$
由于每个区间的密度和颜色都是相同的,因此可以得到:
$$
\int_{t_n}^{t_{n+1}} T(t) \sigma_n C_ndt=\sigma_n C_n \int_{t_n}^{t_{n+1}}T(t)dt
$$
在连续积分推导中得到如下公式:
$$
T(t)=e^{-\int^t_0\sigma(s)ds}
$$
将该公式代入可以得到:
$$
\sigma_nC_n\int_{t_n}^{t_{n+1}}T(t)dt=\sigma_nC_n\int_{t_n}^{t_{n+1}}e^{-\int^t_0\sigma(s)ds}dt
$$
积分内可以进行如下拆分:
$$
e^{-\int_0^t\sigma(s)ds}=e^{-(\int_0^{t_n}\sigma(s)ds+\int_{t_n}^t\sigma(s)ds)}
$$
代入并拆分可以得到:
$$
\sigma_nC_n\int_{t_n}^{t_{n+1}}e^{-\int^t_0\sigma(s)ds}dt=\sigma_nC_n\int_{t_n}^{t_{n+1}}e^{-\int_0^{t_n}\sigma(s)ds}e^{-\int_{t_n}^{t}\sigma(s)ds}dt
$$
不难看出,积分中的前半段与$t$无关,相当于是常数,因此可以单独拿出来:
$$
\sigma_nC_n\int_{t_n}^{t_{n+1}}e^{-\int_0^{t_n}\sigma(s)ds}e^{-\int_{t_n}^{t}\sigma(s)ds}dt=\sigma_nC_nT(0\to t_n)\int_{t_n}^{t_{n+1}}e^{-\int_{t_n}^{t}\sigma(s)ds}dt
$$
由于每一段的密度都是固定的因此$\sigma(s)=\sigma_n$,代入可得:
$$
\sigma_nC_nT(0\to t_n)\int_{t_n}^{t_{n+1}}e^{-\int_{t_n}^{t}\sigma(s)ds}dt=\sigma_nC_nT(0\to t_n)\int_{t_n}^{t_{n+1}}e^{-\int_{t_n}^{t}\sigma_nds}dt
$$
由于$\sigma_n$是常数,因此有如下结论:
$$
-\int_{t_n}^{t}\sigma_nds=-\sigma_n(t-t_n)
$$
代入可得:
$$
\sigma_nC_nT(0\to t_n)\int_{t_n}^{t_{n+1}}e^{-\int_{t_n}^{t}\sigma_nds}dt=\sigma_nC_nT(0\to t_n)\int_{t_n}^{t_{n+1}}e^{-\sigma_n(t-t_n)}dt
$$
计算积分可以得到:
$$
\sigma_nC_nT(0\to t_n)\int_{t_n}^{t_{n+1}}e^{-\sigma_n(t-t_n)}dt=\sigma_n C_n T(0\to t_n)[-\frac{1}{\sigma}e^{-\sigma_n(t-t_n)}\mid_{t_n}^{t_{n+1}}]
$$
将值代入可以得到:
$$
\sigma_n C_n T(0\to t_n)[-\frac{1}{\sigma}e^{-\sigma_n(t-t_n)}\mid_{t_n}^{t_{n+1}}]=C_nT(0\to t_n)[-e^{-\sigma_n(t_{n+1}-t_n)}+e^{-\sigma_n(t_{n}-t_n)}]
$$
由于:
$$
e^{-\sigma_n(t_{n}-t_n)}=e^0=1
$$
因此原式可以化简为:
$$
C_nT(0\to t_n)[-e^{-\sigma_n(t_{n+1}-t_n)}+e^{-\sigma_n(t_{n}-t_n)}]=C_nT(0\to t_n)[1-e^{-\sigma_n(t_{n+1}-t_n)}]
$$
根据之前的描述可以知道每一段的距离都是$\delta_n$,因此:
$$
t_{n+1}-t_n=\delta_n
$$
代入结果可知:
$$
C_nT(0\to t_n)[1-e^{-\sigma_n(t_{n+1}-t_n)}]=C_nT(0\to t_n)(1-e^{-\sigma_n \delta_n})
$$
计算$T(0\to t_n)$:
$$
T(0\to t_n)=e^{-\int_0^{t_n}\sigma(s)ds}=e^{-\sum_{i=0}^{n-1}\sigma_i\delta_i}
$$
将计算结果代入可得:
$$
C_nT(0\to t_n)[1-e^{-\sigma_n \delta_n}]=C_ne^{-\sum_{i=0}^{n-1}\sigma_i\delta_i}(1-e^{-\sigma_n \delta_n})
$$
综上所述,可以得到最终公式:
$$
\hat{C}(r)=\sum^N_{i=1}T_i(1-e^{-\sigma_i\delta_i})C_i
$$
$$
where\ T_i=e^{\sum_{j=1}^{i-1}\sigma_j\delta_j}
$$
在实际代码中,有如下操作:
$$
\alpha_n=1-e^{-\sigma_n\delta_n}
$$
这可以看作第$n$个点的不透明度。
$$
\hat{C}=\sum_{n=0}^{N}C_n\alpha_n(1-\alpha_0)(1-\alpha_1)\dots(1-\alpha_{n-1})
$$
展开可得:
$$
\hat{C}=C_0\alpha_0+C_1\alpha_1(1-\alpha_0)+C_2\alpha_2(1-\alpha_0)(1-\alpha_1)+\dots+C_n\alpha_n(1-\alpha_0)(1-\alpha_1)\dots(1-\alpha_{n-1})
$$
代码
1 | raw2alpha = lambda raw, dists, act_fn=F.relu: 1.-torch.exp(-act_fn(raw)*dists) |
这段代码主要用于体渲染。
1 | raw2alpha = lambda raw, dists, act_fn=F.relu: 1.-torch.exp(-act_fn(raw)*dists) |
这部分代码定义了一个将原始密度值raw转换为不透明度alpha的函数。使用了Relu激活函数确保密度值为非负。
1 | dists = z_vals[...,1:] - z_vals[...,:-1] |
这两行计算相邻采样点之间的距离,并在最后添加一个很大的值$1e10$表示光线延伸到无穷远。这样可以确保光线末端的渲染效果。
1 | dists = dists * torch.norm(rays_d[...,None,:], dim=-1) |
将距离值沿着光线方向标准化,确保在不同的光线方向下距离计算的统一性。
1 | rgb = torch.sigmoid(raw[...,:3]) # [N_rays, N_samples, 3] |
将网络输出的原始颜色值(raw的前三个通道)通过sigmoid函数转换到$(0,1)$范围,符合颜色值的表示要求。
1 | noise = 0. |
为密度值添加随机噪声(用于提高训练稳定性),并在测试时保持结果一致性。
1 | alpha = raw2alpha(raw[...,3] + noise, dists) # [N_rays, N_samples] |
将经过处理的密度值(raw的第四个通道+噪声)转换为不透明度alpha值,同时考虑了采样点之间的距离。raw是模型的输出,前三个通道表示的是RGB,最后一个通道表示的是密度。
1 | # weights = alpha * tf.math.cumprod(1.-alpha + 1e-10, -1, exclusive=True) |
这段代码是核心部分,执行了上述推导的公式:
$$
C_n\alpha_n(1-\alpha_0)(1-\alpha_1)\dots(1-\alpha_{n-1})
$$
1 | rgb_map = torch.sum(weights[...,None] * rgb, -2) # [N_rays, 3] |
对所有采样点的颜色值进行加权求和,得到最终像素颜色值。
综合一下,求得:
$$
\hat{C}=C_0\alpha_0+C_1\alpha_1(1-\alpha_0)+C_2\alpha_2(1-\alpha_0)(1-\alpha_1)+\dots+C_n\alpha_n(1-\alpha_0)(1-\alpha_1)\dots(1-\alpha_{n-1})
$$
需要对每一个通道都求一次权重和,因此最后的结果是一个[N_rays, 3],大小的张量,其中N_rays是射线的数量。
模型输出
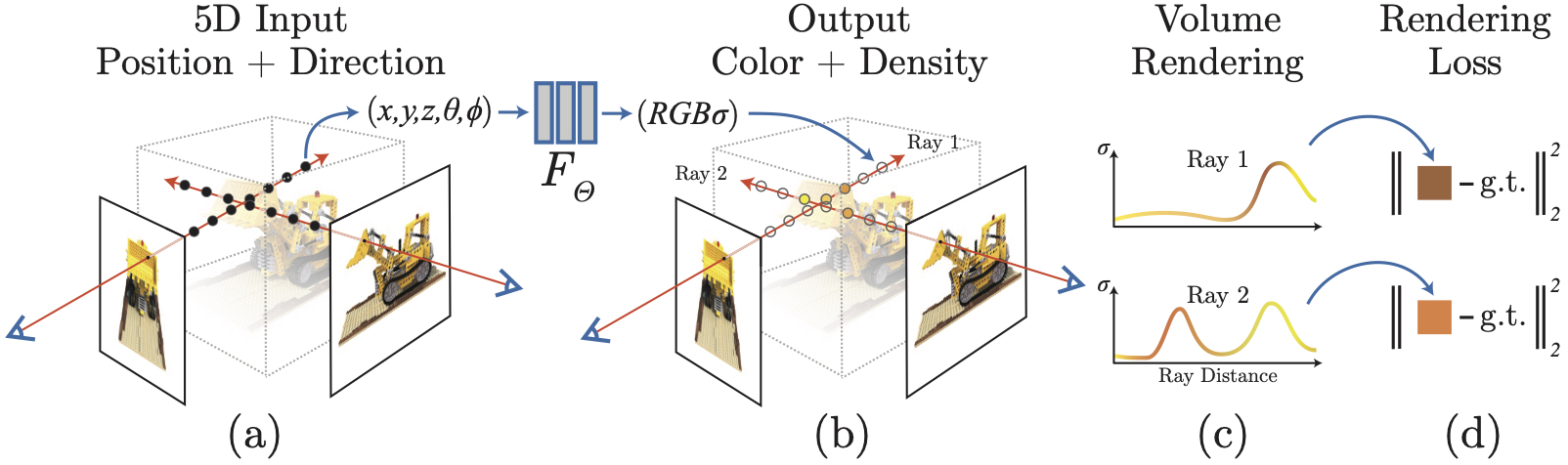
整个渲染流程可以分为几个步骤,首先分别计算图片中每一个像素的颜色,再计算该像素对应的光线和粒子,接着将这些粒子通过公式累加,最终得到该像素的颜色。
最开始只有这些粒子的位姿,并不具备颜色。把这些粒子的位姿输入进模型,模型会去计算这些粒子对应的颜色。预测的时候,通过一排粒子去计算像素的颜色,得到的结果就是预测值,将该值与GT做一个MSE计算Loss。
由于我们是均匀采样的,因此会有许多的无效区域(空白区域和遮挡区域)。为了能够让模型效果更好,希望能够在有效区域多采样,无效区域少采样或者不采样。
二次采样
逆变换采样流程
为了解决这一问题,可以根据概率密度进行再次采样。实际上的NeRF模型是将两个$8$层的MLP多层感知机串联起来,第一个MLP叫粗模型,第二个MLP叫细模型。
粗模型输入均匀采样粒子,输出密度;细模型根据密度进行二次采样。最后的输出采用细模型的输出,这两个模型结构相同。
解决方法:
- 根据粗模型的结果,进行逆变换采样。
- 对于每条光线,重新采样$128$个粒子。
- 与之前的$64$个粒子加在一起。
- 即每条光线采样$192$个粒子。
首先根据权重归一化公式:
$$
\hat{w_i}=\frac{w_i}{\sum_{j=1}^{N_c}w_j}
$$
通过这个公式,对于每条射线上的粒子颜色前的权重做softmax;此时,新的权重和为$1$,可以看做PDF(概率密度函数);根据概率密度函数生成CDF(累积分布函数);计算CDF的反函数,用均匀分布生成随机数得到$r$,该值就是符合PDF分布的随机数。
代码
1 | def sample_pdf(bins, weights, N_samples, det=False, pytest=False): |
这段代码实现了NeRF中基于累积分布函数(CDF)的逆变换采样功能,是分层采样的核心技术。
1 | def sample_pdf(bins, weights, N_samples, det=False, pytest=False): |
这部分代码将权重转换为概率密度函数(PDF)和累积分布函数(CDF)
- 添加小量(1e-5)避免除零错误
- 计算归一化概率密度函数:
pdf = 权重/总权重 - 生成累积分布函数:通过累加前面的概率
- 添加起点0(在CDF前填充一个0值)
1 | # Take uniform samples |
这段代码生成均匀分布的随机数:
- 当
det=True时,生成等间隔的样本(用于可视化) - 当
det=False时,生成均匀随机样本(默认训练模式) - 扩展张量维度以匹配批量大小
1 | # Pytest, overwrite u with numpy's fixed random numbers |
这段代码用于测试时保持一致结果:
- 固定随机种子(0)确保结果可重现
- 根据测试模式选择固定或随机样本
- 将numpy数组转换为PyTorch张量
1 | # Invert CDF |
这部分实现逆变换的核心逻辑:
- 确保内存连续(优化性能)
- 找到u值在
CDF中的位置inds - 计算区间索引:
below(下界)和above(上界) - 组合为成对索引[below, above]
1 | # cdf_g = tf.gather(cdf, inds_g, axis=-1, batch_dims=len(inds_g.shape)-2) |
这段代码提取关键数据:
- 匹配张量形状为[批量大小, 样本数, 维度数]
- 通过
gather操作提取CDF边界值 - 提取深度区间边界值
bins_g
1 | denom = (cdf_g[...,1]-cdf_g[...,0]) |
最后部分进行线性插值:
- 计算
CDF区间长度denom - 避免除零错误(
denom过小时设为$1$) - 计算插值比例
t - 在深度区间内线性插值得到最终样本位置
推理
上述主要是训练部分,推理相当于给一张固定大小($H\times W$)的空白图片,那么一共有$H\times W$条射线,上面分别采样$N$个点。
通过粗模型和细模型,最后的输出为$[H\times W\times N \times 3, 4]$,具体为每个采样粒子的颜色和密度,最后根据这些数据进行体渲染。
总结
前处理
将图片中的每个像素,通过相机模型找到对应的射线,在每条射线上的采样,得到$64$个粒子。
对batch_size * 64个粒子进行位置编码(默认batch_size为$1024$),位置坐标变为$63D$,方向向量变为$27D$。
模型1
第一个是粗模型,是一个$8$层的MLP。输入为$(1024,64,63)$和$(1024,64,27)$;输出为$(1024,64,4)$。
后处理1
计算粗模型的输出,对射线进行二次采样,每条射线上共采样$192$个粒子。
模型2
第二个是细模型,同样是一个$8$层的MLP。输入为$(1024,192,63)$和$(1024,192,27)$;输出为$(1024,192,4)$。
后处理2
将细模型的输出通过体渲染,转换为像素。
核心内容
核心内容主要有三个,分别是体渲染,位置编码和层级采样。
缺点
- 训练和推理的速度都非常慢。
- 只能表达静态场景。
- 对光照处理的一般(方位角是后输入的)。
- 没有泛化能力。
渲染测试
采用官网预训练好的模型和lego数据集,分别使用两种不同的渲染参数。
官方渲染
首先是官方的渲染参数,使用RTX4060,参数为:
1 | expname = lego_test |
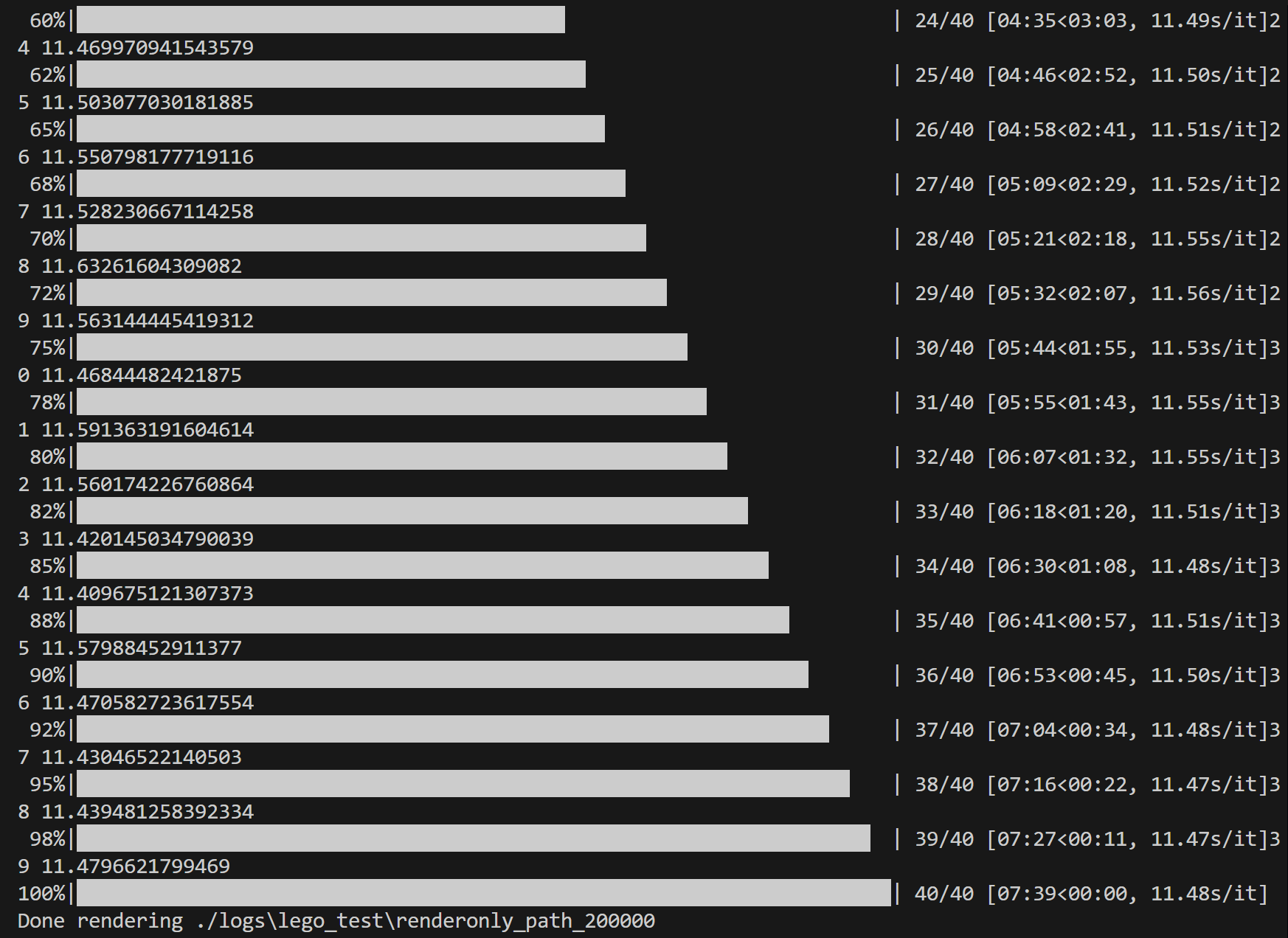
可以看到渲染一张图片需要的时间大概需要$11.5$秒。
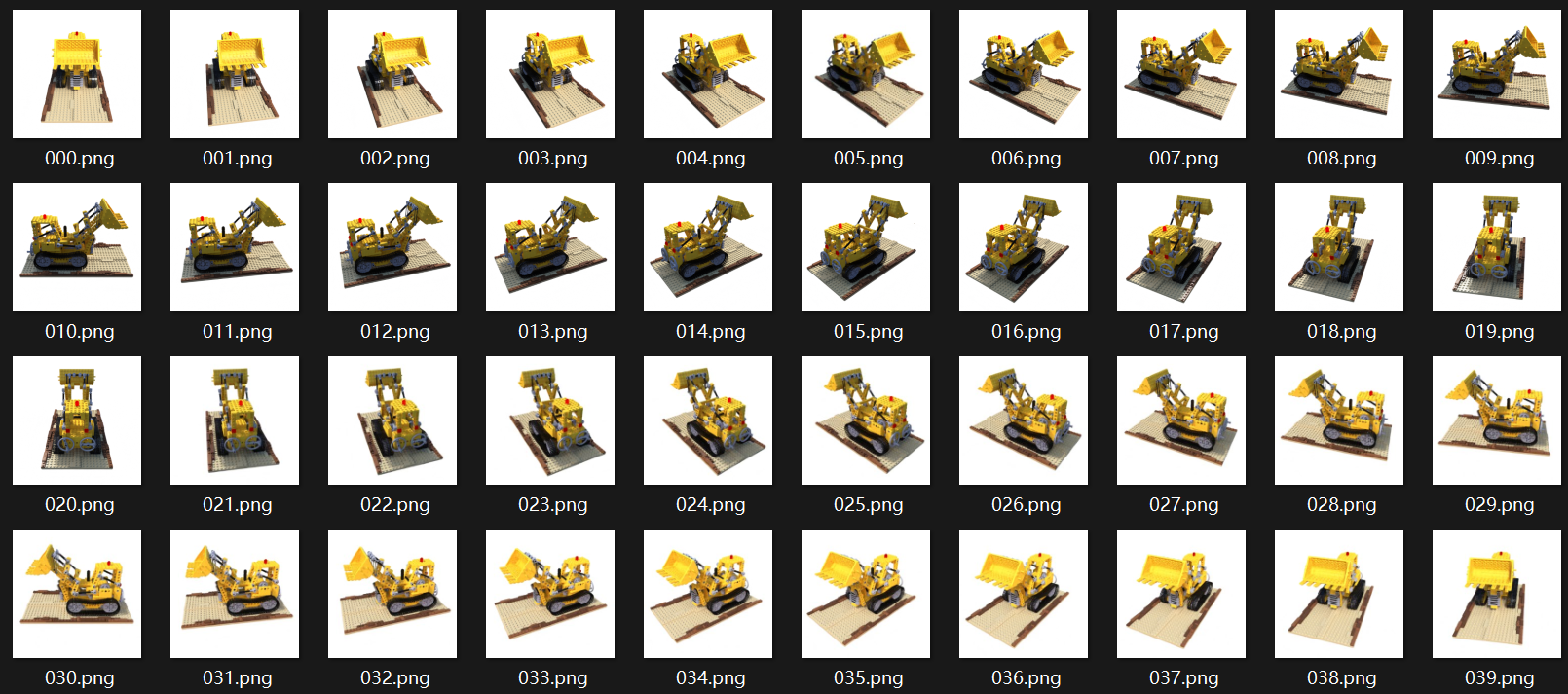
加强渲染
官方的渲染参数效果没有那么好,可以修改为如下参数,从而提高精度:
1 | expname = lego_test |
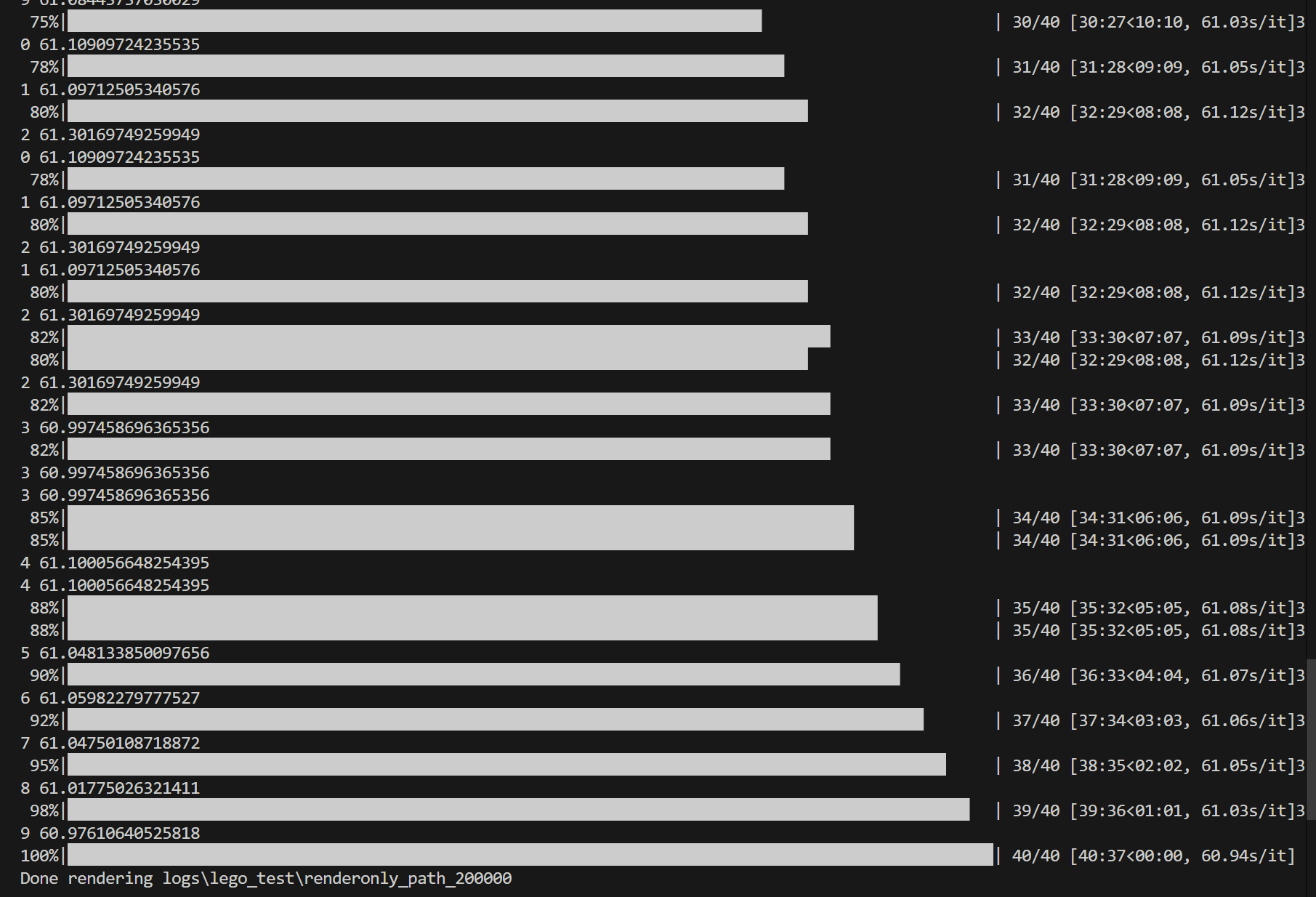
可以看到渲染一张图片需要的时间大概需要$61$秒。